

The four triangles with area abĪlso form a larger square with sides of length c. In the second orientation shown in the figure, ii, the four copies of the same triangle are arranged such that they form an enclosed square with sides of length b - a, and area (b - a) 2. The sum of the area of these four triangles and the smaller square must equal the area of the larger square such that: (b + a) 2 = c 2 + 4

This results in the formation of a larger square with sides of length b + a, and area of (b + a) 2.
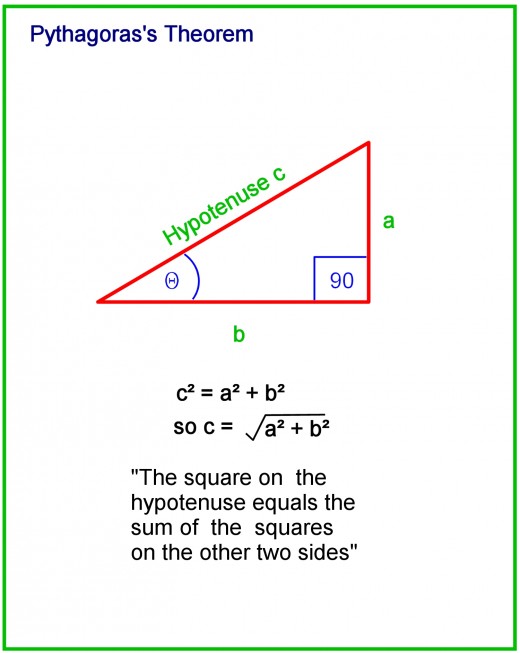
In the first one, i, the four copies of the same triangle are arranged around a square with sides c. In the figure above, there are two orientations of copies of right triangles used to form a smaller and larger square, labeled i and ii, that depict two algebraic proofs of the Pythagorean theorem. There are a multitude of proofs for the Pythagorean theorem, possibly even the greatest number of any mathematical theorem. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation. The law of cosines is a generalization of the Pythagorean theorem that can be used to determine the length of any side of a triangle if the lengths and angles of the other two sides of the triangle are known. It follows that the length of a and b can also be determined if the lengths of the other two sides are known using the following relationships: This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. In other words, given that the longest side c = the hypotenuse, and a and b = the other sides of the triangle: Given a right triangle, which is a triangle in which one of the angles is 90°, the Pythagorean theorem states that the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right triangle: The Pythagorean Theorem, also known as Pythagoras' theorem, is a fundamental relation between the three sides of a right triangle. Mag., 73(2000), 259-272.Related Triangle Calculator | Right Triangle Calculator Velian, “The 2500-Year-Old Pythagorean Theorem”, Math. “Spherical Pythagorean Theorem.” Math Fun Facts.ĭ. Can you guess what it says? See the reference. This formula is called the “Spherical Pythagorean Theorem” because the regular Pythagorean theorem can be obtained as a special case: as R goes to infinity, expanding the cosines using their Taylor series and manipulating the resulting expression will yield:Īs R goes to infinity! This should make sense, since as R goes to infinity, spherical geometry becomes more and more like regular planar geometry!īy the way, there is a “hyperbolic geometry” version, too. For more on spherical triangles, see the Fun Fact on Spherical Geometry. Verify the formula is true in some simple examples: such a triangle with two right angles formed by the equator and two longitudes. Then the following particularly nice formula holds:

Let A and B denote the lengths of the other two sides. In such a triangle, let C denote the length of the side opposite right angle. If one of the corner angles is a right angle, the triangle is a spherical right triangle. A spherical triangle is any 3-sided region enclosed by sides that are arcs of great circles. A great circle on a sphere is any circle whose center coincides with the center of the sphere. Did you know there is a version of the Pythagorean Theorem for right triangles on spheres?įirst, let’s define precisely what we mean by a spherical triangle.


 0 kommentar(er)
0 kommentar(er)
